Usage Example - Operation: 'MO 3'

Model Volume Creation

Procedure used: mo3.spi

.OPERATION MO 3 ;   Model volume creation
.OUTPUT FILE NAME mo_3_c ;   New file name
.ENTER DIMENSIONS 150,150,150 ;   Size of volume
.ENTER (B/C/H/HA/G/G1/G2/G3/NUM/R/S/SP/SPA/SPV/T/W) C ;   Model cylinder
.DENSITY VALUE OUTSIDE CYLINDER 0 ;   Background
.CHOOSE X, Y, Z (OR Q TO END CYLINDER ENTRY): Y ;   Cylinder axis
.RADIUS, HEIGHT: 17,75 ;   Cylinder radius, height
.X, Y COORDINATES OF CENTER: 75,75 ;   Cylinder center in X & Y
.Z COORDINATE, DENSITY: 75,1 ;   Z Center, cylinder density
.CHOOSE X, Y, Z (OR Q TO END CYLINDER ENTRY): X ;   Next cylinder axis
.RADIUS, HEIGHT: 10,99 ;   Cylinder radius, height
.X & Y COORDINATES OF CENTER: 75,75 ;   Cylinder center in X & Y
.Z COORDINATE, DENSITY: 75,1 ;   Z Center, cylinder density
.CHOOSE X, Y, Z (OR Q TO END CYLINDER ENTRY): Q ;   Quit making cylinders


OUTPUT
mo_3_c


Usage Example - Operation: MO 3 Option: H (Helix of spheres)

Model Volume Creation

Procedure used: mo3.spi

.OPERATION: MO 3 ;   Model volume creation
.OUTPUT FILE NAME: mo_3_h ;   New file name
.DIMENSIONS: 150,150,150 ;   Size of volume
.OPTION (B/C/H/HA/G/G1/G2/G3/NUM/R/S/SP/SPA/SPV/T/W): H ;   Helix of spheres
.DENSITY INSIDE SPHERES (or <CR> = 2.0) 1 ;   Sphere intensities
.SPHERE RADIUS, HELIX RADIUS: 5,20 ;   Sphere radius, helix radius
.NO. OF SPHERES, NO. OF TURNS: 24, 3 ;   No. of spheres, turns


OUTPUT
mo_3_h


Usage Example - Operation: MO 3 Option: G1,G2,G3 (Gaussian masks)

Model Volume Creation

Procedure used: mo3.spi

.OPERATION: MO 3 ;   Model volume creation
.OUTPUT FILE NAME: mo_3_g1 ;   New file name
.DIMENSIONS: 250,250,250 ;   Size of volume
.OPTION (B/C/H/HA/G/G1/G2/G3/NUM/R/S/SP/SPA/SPV/T/W): G1 ;   Gaussian sphere
.CENTER COORDINATES X,Y,Z: 85,85,75 ;   Center in X, Y, & Z
.RADII IN X,Y,Z ( = STD. DEV.): 2, 3, 4 ;   Radii in X, Y, & Z


Following illustrations show the properties of Super-Gaussian masks using 2D masks.

Fig. 1. Different 2D masks.
Fig. 2. Profiles of different 2D masks along one diameter.
Fig. 3. Profiles of Fourier Transforms of different 2D masks along one diameter.

OUTPUT
Fig. 1. Different 2D masks

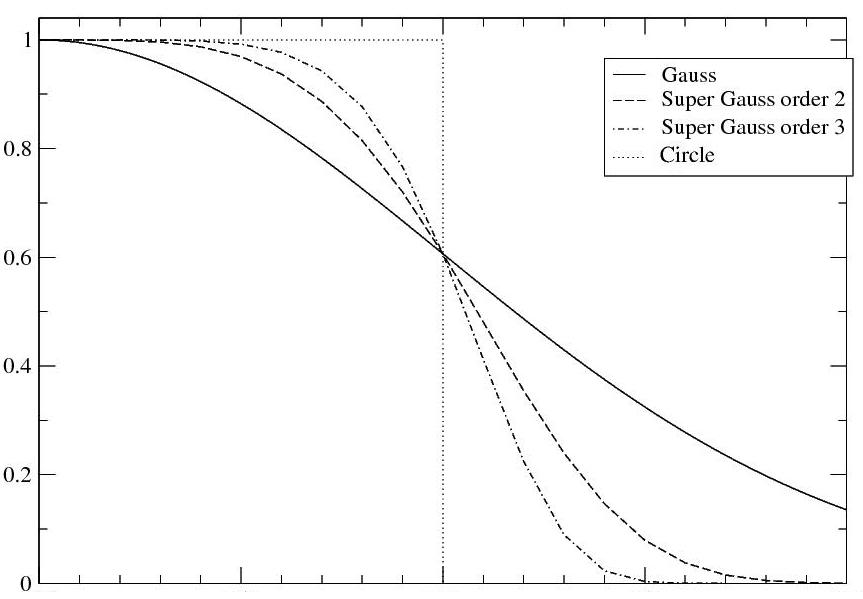Fig. 2. Profiles of different 2D masks along one diameter.

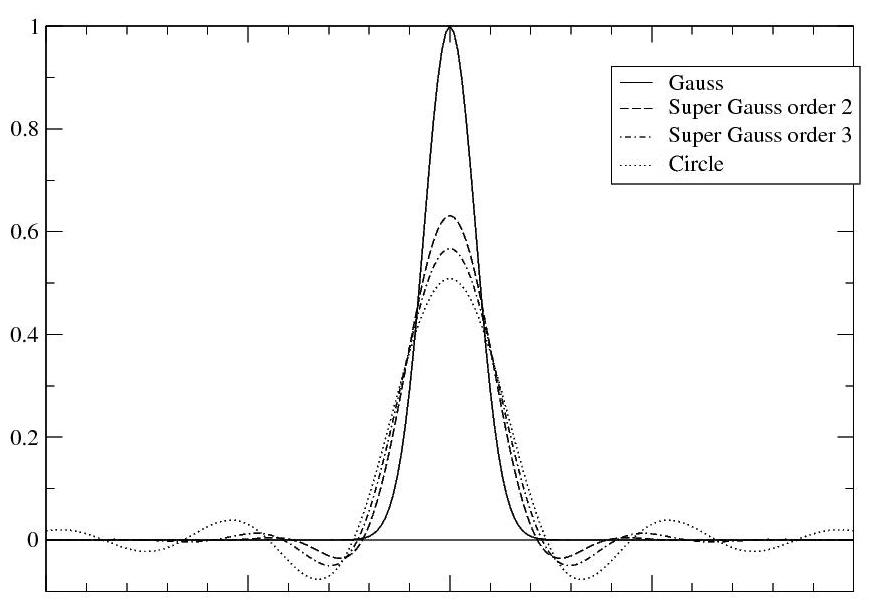Fig. 3. Profiles of Fourier Transforms of different 2D masks along one diameter.